Ponto, reta e plano

Euclides estudou os elementos primitivos (ponto, reta e plano) e formulou a Geometria Euclidiana. 
Representamos o ponto por qualquer letra maiúscula do alfabeto, a reta por qualquer letra minúscula e o plano por letras gregas (α: alfa, β: beta e γ: gama). 

Ponto: o ponto pode ser algo localizado no espaço, como um furo, uma estrela no céu, o centro do campo de futebol, etc.

Reta: podemos dizer que a reta é formada por infinitos pontos, como uma caneta, uma corda esticada, lados de um campo de futebol, as traves do gol, os raios solares, etc.

Plano: a superfície de uma parede, o chão, um quadro, universo, etc.

Representação, (notação)

→ Pontos serão representados por letras latinas maiúsculas; ex: A, B, C,...
→ Retas serão representados por letras latinas minúsculas; ex: a, b, c,...
→ Planos serão representados por letras gregas minúsculas; ex:

Representação gráfica

Postulados primitivos da geometria, qualquer postulado ou axioma é aceito sem que seja necessária a prova, contanto que não exista a contraprova.

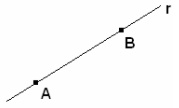
1º Numa reta bem como fora dela há infinitos pontos distintos.



2º Dois pontos determinam uma única reta (uma e somente uma reta).

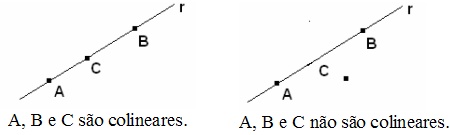
3º Pontos colineares pertencem à mesma reta.

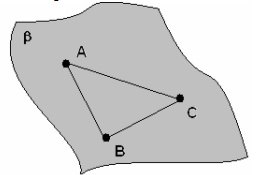
4º Três pontos determinam um único plano.

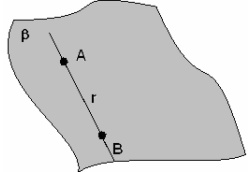
5º Se uma reta contém dois pontos de um plano, esta reta está contida neste plano.

6º Duas retas são concorrentes se tiverem apenas um ponto em comum.

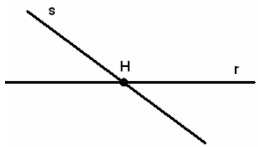
7º Retas que não possuem nenhum ponto em comum são retas paralelas. 

8º Perpendiculares: retas que possuem um ponto em comum e formam um ângulo de 90º.

9º Uma semirreta possui origem em um ponto, tornando-se infinita no sentido contrário. 

                                                         

10º Um segmento de reta: possui origem e fim. 

Essas definições serão introduzidas em Geometria Analítica, posteriorizando um estudo mais detalhado de todos os elementos no espaço, distância entre: dois pontos, entre ponto e reta, entre duas retas, ponto médio entre segmentos e outras situações.