Resposta do exercício sobre trigonometria

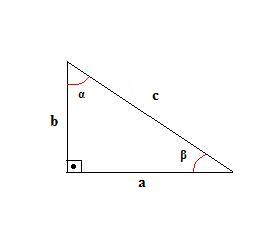
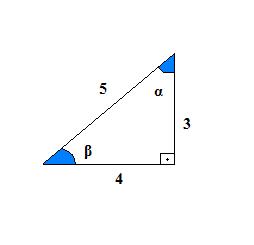
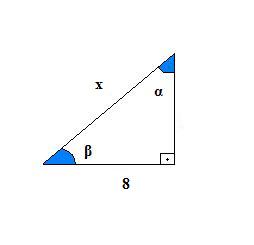
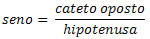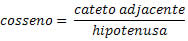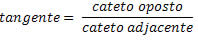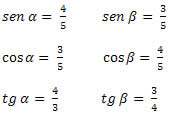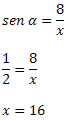Espero que vocês tenham acertado as respostas. 

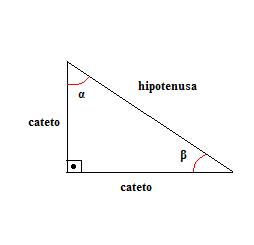
Questão A

cos 65° = y / 9

0,42 * 9 = y

y = 3,78

sen 65° = x /9

0,91 * 9 = x

x = 8,19

Questão B

sen 60° = 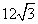 / a

0,866 . a = 20,78

a = 24

cos 60° = b / 24

0,5 * 24 = b

b = 12

Questão C

Questão D

tg  = 48 / 14 = 24 / 7

tg Ê = 14 / 48 = 7 / 24

Questão E

tg Ô = 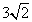/  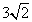= 1

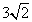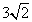tg Ê = /  = 1

Questão F

16² = 2² + x²

x² = 252

x =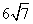 

tg  = 2 / 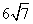= 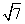/ 21

tg Ô = 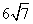/ 2 = 3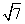

Questão G

Se sabemos que é um triângulo isósceles, então seus lados são iguais. Logo, tg  = 1 e tg Ê = 1.

Questão H

3 = 9 / x

3x = 9

x = 3

(RA)² = 9² + 3²

(RA)² = 90

(RA) =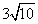 

Questão I

cos 45° = x /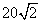 

 *  = x

x = 20

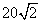()² = 20² + y²

800 = 400 + y²

y² = 400

y = 20

Questão J

cos 30° = / y




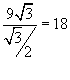
y = 18

18² = (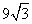)² + x²

324 = 243 + x²

x² = 81

x = 9

Exercícios de Razões Trigonométricas

Exercícios de Razões Trigonométricas

a) No triângulo retângulo da figura abaixo, determine as medidas de x e y indicadas (Use: sen 65° = 0,91; cos 65° = 0,42 ; tg 65° = 2,14) b) Considerando o triângulo retângulo ABC da figura, determine as medidas a e b indicadas. (Sen 60° = 0,866) c) Sabe-se que, em um triângulo retângulo isósceles, cada lado congruente mede 30 cm. Determine a medida da hipotenusa desse triângulo. Nos triângulos das figuras abaixo, calcule tg Â, tg Ê, tg Ô: d)                             e)       f)  g) Sabendo que o triângulo retângulo da figura abaixo é isósceles, quais são os valores de tg  e tg Ê? h) Encontre a medida RA sabendo que tg  = 3. Encontre x e y: i)          j)

Trigonometria no triangulo retângulo

A trigonometria é uma ferramenta matemática bastante utilizada no cálculo de distâncias envolvendo triângulos retângulos. Na antiguidade, matemáticos utilizavam o conhecimento adquirido em trigonometria para realizar cálculos ligados à astronomia, determinando a distância, quase que precisa, entre a Terra e os demais astros do sistema solar. Atualmente a trigonometria também é bastante utilizada e para compreender o seu uso é necessário assimilar alguns conceitos.

Observe a figura abaixo que representa um triângulo retângulo.

Note que o maior lado é denominado de hipotenusa e os outros dois lados de catetos. A hipotenusa é o lado que fica oposto ao ângulo reto (ângulo de 90^o). Além do ângulo reto, há dois ângulos agudos, α e β. A trigonometria estabelece relações entre os ângulos agudos do triângulo retângulo e as medidas de seus lados. Vejamos quais são essas relações.

O seno de um ângulo no triângulo retângulo é a razão entre o cateto oposto e a hipotenusa.

O cosseno de um ângulo no triângulo retângulo é a razão entre o cateto adjacente e a hipotenusa.

A tangente de um ângulo no triângulo retângulo é a razão entre o cateto oposto e o cateto adjacente.

Definidas as razões trigonométricas, obtemos as seguintes igualdades para o triângulo retângulo abaixo:

Exemplo 1. Determine os valores de seno, cosseno e tangente dos ângulos agudos do triângulo abaixo:

Solução: Temos que

Exemplo 2. Sabendo que sen α =1/2 , determine o valor de x no triângulo retângulo abaixo:

Solução: A hipotenusa do triângulo é x e o lado com medida conhecida é o cateto oposto ao ângulo α. Assim, temos que: