Posições relativas de duas Retas

As figuras planas e espaciais são formadas pela intersecção de retas e planos pertencentes ao espaço. Dentre as posições relativas, podemos destacar:

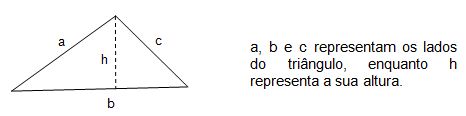
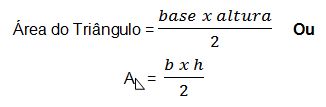Posição relativa entre duas retas

Duas retas distintas irão assumir as seguintes posições relativas no espaço:

Retas paralelas: duas retas são paralelas se pertencerem ao mesmo plano (coplanares) e não possuírem ponto de intersecção ou ponto em comum.

Retas coincidentes: pertencem ao mesmo plano e possuem todos os pontos em comum.

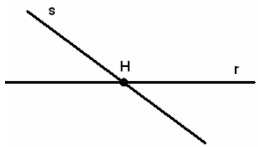
Retas concorrentes: duas retas concorrentes possuem apenas um ponto comum. Não é necessário que pertençam ao mesmo plano.

Retas concorrentes perpendiculares: são retas que possuem ponto em comum formando um ângulo de 90º.

Retas reversas: estão presentes em planos distintos.

Posição relativa entre reta e plano.

Uma reta e um plano poderão ter as seguintes posições relativas:

Reta paralela ao plano: considere uma reta t e um plano β, eles serão paralelos se não tiverem nenhum ponto em comum.

Reta contida no plano: considerando uma reta t e um plano β. t está contido em β se todos os infinitos pontos de t pertencerem a β.

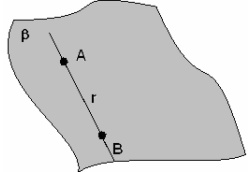
Retas e planos secantes ou concorrentes: a reta t será concorrente ao plano β se possuírem um ponto em comum.

Posição entre dois planos

Dois planos irão assumir no espaço as seguintes posições relativas entre si:

Planos paralelos: dois planos são considerados paralelos se não possuírem pontos em comum ou se uma reta pertencente ao plano α (alfa) for paralela a uma reta pertencente ao plano β (beta).

Planos secantes: dois planos são secantes quando forem distintos e a intersecção entre eles formar uma reta.

Planos coincidentes: planos coincidentes equivalem a um mesmo plano, ou seja, todos os seus infinitos pontos e planos pertencem ao outro.

Ponto, reta e plano

Euclides estudou os elementos primitivos (ponto, reta e plano) e formulou a Geometria Euclidiana. 
Representamos o ponto por qualquer letra maiúscula do alfabeto, a reta por qualquer letra minúscula e o plano por letras gregas (α: alfa, β: beta e γ: gama). 

Ponto: o ponto pode ser algo localizado no espaço, como um furo, uma estrela no céu, o centro do campo de futebol, etc.

Reta: podemos dizer que a reta é formada por infinitos pontos, como uma caneta, uma corda esticada, lados de um campo de futebol, as traves do gol, os raios solares, etc.

Plano: a superfície de uma parede, o chão, um quadro, universo, etc.

Representação, (notação)

→ Pontos serão representados por letras latinas maiúsculas; ex: A, B, C,...
→ Retas serão representados por letras latinas minúsculas; ex: a, b, c,...
→ Planos serão representados por letras gregas minúsculas; ex:

Representação gráfica

Postulados primitivos da geometria, qualquer postulado ou axioma é aceito sem que seja necessária a prova, contanto que não exista a contraprova.

1º Numa reta bem como fora dela há infinitos pontos distintos.



2º Dois pontos determinam uma única reta (uma e somente uma reta).

3º Pontos colineares pertencem à mesma reta.

4º Três pontos determinam um único plano.

5º Se uma reta contém dois pontos de um plano, esta reta está contida neste plano.

6º Duas retas são concorrentes se tiverem apenas um ponto em comum.

7º Retas que não possuem nenhum ponto em comum são retas paralelas. 

8º Perpendiculares: retas que possuem um ponto em comum e formam um ângulo de 90º.

9º Uma semirreta possui origem em um ponto, tornando-se infinita no sentido contrário. 

                                                         

10º Um segmento de reta: possui origem e fim. 

Essas definições serão introduzidas em Geometria Analítica, posteriorizando um estudo mais detalhado de todos os elementos no espaço, distância entre: dois pontos, entre ponto e reta, entre duas retas, ponto médio entre segmentos e outras situações.

O trapézio

O trapézio é uma figura plana com um par de lados paralelos (bases) e um par de lados concorrentes.

Geometria Plana - Continuação

O triângulo

O triângulo é uma figura geométrica plana formada por três lados e três ângulos. A soma dos seus ângulos internos é igual 180º.

Para calcular a área do triângulo multiplica-se a base b (base) pela altura h (altura) e divide o resultado por 2 (metade da área do retângulo).

Exemplo

Encontre a área de um triângulo cuja base mede 8,2 cm e a altura 3,6 cm.